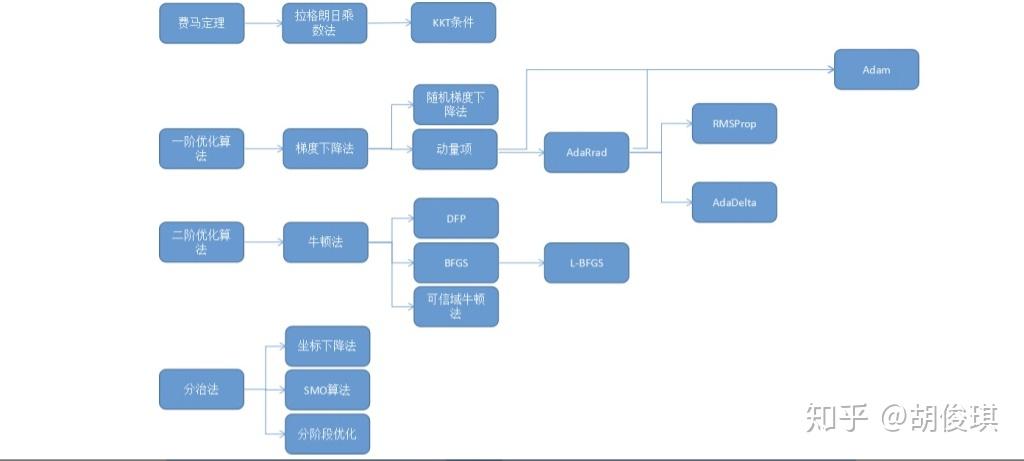
我们都知道机器学习的三要素:模型， 策略， 算法。在这三个关键步骤中，前两个是机器学习要研究的问题，建立数学模型。第三个问题是纯数学问题，即最优化方法，为本文所讲述的核心。

1. 公式解
2. 数值优化

前者给出一个最优化问题精确的公式解，也称为解析解，一般是理论结果。后者是在要给出极值点的精确计算公式非常困难的情况下，用数值计算方法近似求解得到最优点。除此之外，还有其他一些求解思想，如分治法，动态规划等。我们在后面单独列出。

一个好的优化算法需要满足：

1. 能正确的找到各种情况下的极值点
2. 速度要快

对于一个可导函数，寻找其极值的统一做法是寻找导数为0的点，即费马定理。微积分中的这一定理指出，对于可导函数，在极值点处导数必定为0：

对于多元函数，则是梯度为0:

导数为0的点称为驻点。需要注意的是，导数为0只是函数取得极值的必要条件而不是充分条件，它只是疑似极值点。是不是极值，是极大值还是极小值，还需要看更高阶导数。对于一元函数，假设x是驻点：

1.如果 (x)＞0，则在该点处去极小值

2.如果 (x)＜0，则在该点处去极大值

3.如果 (x)＝0，还要看更高阶导数

对于多元函数，假设x是驻点：

1.如果Hessian矩阵正定，函数在该点有极小值

2.如果Hessian矩阵负定，函数在该点有极大值

3.如果Hessian矩阵不定，则不是极值点

Problem:

1. 在导数为0的点处，函数可能不取极值，这称为鞍点。
2. 有可能是局部极值点，而不是全局极值点。

费马引理给出的是不带约束条件下的函数极值的必要条件。

而对于带有等式约束的极值问题，则是拉格朗日乘数法。

KKT条件是拉格朗日乘数法的推广，用于求解既带有等式约束，又带有不等式约束的函数极值。对于如下优化问题：

前面讲述的三种方法在理论推导、某些可以得到方程组的求根公式的情况（如线性函数，正态分布的最大似然估计）中可以使用，但对绝大多数函数来说，梯度等于0的方程组是没法直接解出来的，如方程里面含有指数函数、对数函数之类的超越函数。对于这种无法直接求解的方程组，我们只能采用近似的算法来求解，即数值优化算法。这些数值优化算法一般都利用了目标函数的导数信息，如一阶导数和二阶导数。如果采用一阶导数，则称为一阶优化算法。如果使用了二阶导数，则称为二阶优化算法。

工程上实现时通常采用的是迭代法，它从一个初始点 开始，反复使用某种规则从 移动到下一个点 ，构造这样一个数列，直到收敛到梯度为0的点处。即有下面的极限成立：

1.Gradient Descent：

梯度下降法沿着梯度的反方向进行搜索，利用了函数的一阶导数信息。梯度下降法的迭代公式为：

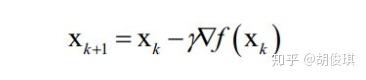
2.AdaGrad算法

AdaGrad算法是梯度下降法最直接的改进。梯度下降法依赖于人工设定的学习率，如果设置过小，收敛太慢，而如果设置太大，可能导致算法那不收敛，为这个学习率设置一个合适的值非常困难。

AdaGrad算法根据前几轮迭代时的历史梯度值动态调整学习率，且优化变量向量x的每一个分量 都有自己的学习率。参数更新公式为：

其中 是学习因子， 是第t次迭代时参数的梯度向量， 是一个很小的正数，为了避免除0操作，下标i表示向量的分量。和标准梯度下降法唯一不同的是多了分母中的这一项，它累积了到本次迭代为止梯度的历史值信息用于生成梯度下降的系数值。根据上式，历史导数值的绝对值越大分量学习率越小，反之越大。虽然实现了自适应学习率，但这种算法还是存在问题：需要人工设置一个全局的学习率 ，随着时间的累积，上式中的分母会越来越大，导致学习率趋向于0，参数无法有效更新。

3.RMSProp算法

4.AdaDelta

5.Adam

假设训练样本集有N个样本，有监督学习算法训练时优化的目标是这个数据集上的平均损失函数：

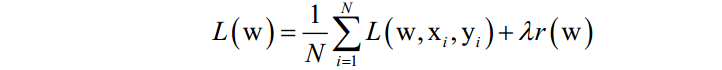
其中L(w, , )是对单个训练样本( , )的损失函数，w是需要学习的参数，r(w)是正则化项， 是正则化项的权重。在训练样本数很大时，如果训练时每次迭代都用所有样本，计算成本太高，作为改进可以在每次迭代时选取一批样本，将损失函数定义在这些样本上。

批量随机梯度下降法在每次迭代中使用上面目标函数的随机逼近值，即只使用M N个随机选择的样本来近似计算损失函数。在每次迭代时要优化的目标函数变为：

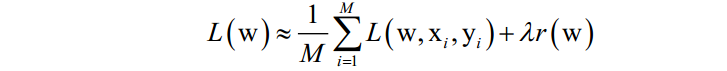
随机梯度下降法在概率意义下收敛。

牛顿法是二阶优化技术，利用了函数的一阶和二阶导数信息，直接寻找梯度为0的点。牛顿法的迭代公式为：

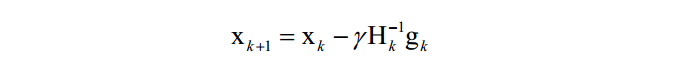
其中H为Hessian矩阵，g为梯度向量。牛顿法不能保证每次迭代时函数值下降，也不能保证收敛到极小值点。在实现时，也需要设置学习率，原因和梯度下降法相同，是为了能够忽略泰勒展开中的高阶项。学习率的设置通常采用直线搜索（line search）技术。

在实现时，一般不直接求Hessian矩阵的逆矩阵，而是求解下面的线性方程组：

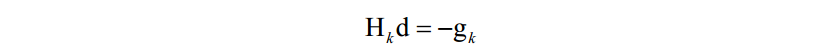
其解d称为牛顿方向。迭代终止的判定依据是梯度值充分接近于0，或者达到最大指定迭代次数。

牛顿法比梯度下降法有更快的收敛速度，但每次迭代时需要计算Hessian矩阵，并求解一个线性方程组，运算量大。另外，如果Hessian矩阵不可逆，则这种方法失效。

牛顿法在每次迭代时需要计算出Hessian矩阵，并且求解一个以该矩阵为系数矩阵的线性方程组，Hessian矩阵可能不可逆。为此提出了一些改进的方法，典型的代表是拟牛顿法。拟牛顿法的思路是不计算目标函数的Hessian矩阵然后求逆矩阵，而是通过其他手段得到一个近似Hessian矩阵逆的矩阵。具体做法是构造一个近似Hessian矩阵或其逆矩阵的正定对称矩阵，用该矩阵进行牛顿法的迭代。

分治法是一种算法设计思想，它将一个大的问题分解成子问题进行求解。根据子问题解构造出整个问题的解。在最优化方法中，具体做法是每次迭代时只调整优化向量x的一部分分量，其他的分量固定住不动。

SMO算法也是一种分治法，用于求解支持向量机的对偶问题。加上松弛变量和核函数后的对偶问题为：

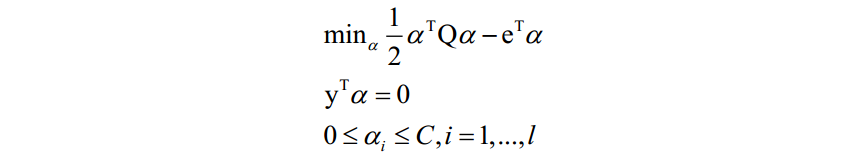
SMO算法的核心思想是每次在优化变量中挑出两个分量 和 进行优化，让其他分量固定，这样能保证满足等式约束条件。之所以要选择两个变量进行优化而不是选择一个变量，是因为这里有等式约束，如果只调整一个变量的值，将会破坏等式约束。

假设选取的两个分量为 和 ，其他分量都固定即当成常数。对这两个变量的目标函数是一个二元二次函数。这个问题还带有等式和不等式约束条件。对这个子问题可以直接求得公式解，就是某一区间内的一元二次函数的极值。

分阶段优化的做法是在每次迭代时，先固定住优化变量x一部分分量a不动，对另外一部分变量b进行优化；然后再固定住b不动，对b进行优化。如此反复，直至收敛到最优解处。

AdaBoost算法是这种方法的典型代表。AdaBoost算法在训练时采用了指数损失函数：

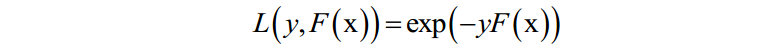
由于强分类器是多个弱分类器的加权和，代入上面的损失函数中，得到算法训练时要优化的目标函数为：

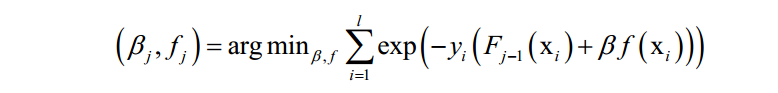
这里将指数损伤函数拆成了两部分，已有的强分类器 ，以及当前弱分类器f对训练样本的损失函数，前者在之前的迭代中已经求出，因此可以看成常数。这样目标函数可以简化为：

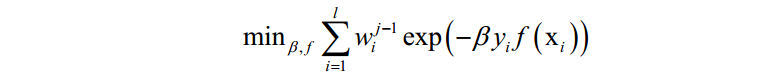
其中：

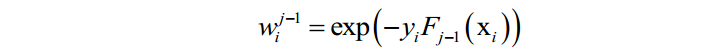
这个问题可以分两步求解，首先将弱分类器权重 看成常数，得到最优的弱分类器f。得到弱分类器之后，再优化它的权重系数 。

动态规划也是一种求解思想，它将一个问题分解成子问题求解，如果整个问题的某个解是最优的，则这个解的任意一部分也是子问题的最优解。这样通过求解子问题，得到最优解，逐步扩展，最后得到整个问题的最优解。

隐马尔可夫模型的解码算法（维特比算法），强化学习中的动态规划算法是这类方法的典型代表，此类算法一般是离散变量的优化，而且是组合优化问题。前面讲述的基于导数的优化算法都无法使用。动态规划算法能高效的求解此类问题，其基础是贝尔曼最优化原理。一旦写成了递归形式的最优化方程，就可以构造算法进行求解。

参考博客:https://zhuanlan.zhihu.com/p/42689565